How Do You Find The Range In A Quadratic Function

Hey there, math buddy! So, we’re gonna talk about quadratic functions. Yeah, I know, they sound a little… intense. Like something you’d find in a secret agent manual, right? But honestly, they’re not that scary. Think of them as those cool U-shaped or upside-down U-shaped graphs. You’ve probably seen them, haven’t you? They’re everywhere once you start looking!
Today, our mission, should we choose to accept it (and we totally should, it’s not that hard), is to figure out the range of these functions. What’s the range, you ask? Oh, it’s just the set of all possible y-values your graph can reach. Like, what’s the lowest point it goes, or the highest? Or maybe it just goes on forever in both directions, who knows!
So, let’s dive in, shall we? Grab your metaphorical coffee cup, settle in, and let’s untangle this quadratic mystery together.
The Big Picture: What’s a Quadratic Function Anyway?
Before we get to the range, we gotta know what we’re dealing with. A quadratic function is basically an equation where the highest power of x is a 2. You know, like ax² + bx + c. That a, b, and c? They’re just numbers, coefficients, fancy words for multipliers and add-ins. And that a? It’s kind of the VIP here. It tells us a whole lot about our graph.
If a is a positive number (like 2, 5, or even a tiny decimal like 0.1), our U-shape will be opening upwards. Think of a happy smiley face! 😊 It has a lowest point, a minimum. It just keeps going up and up and up after that, towards infinity, like a rocket launch! 🚀
Now, if a is a negative number (like -3, -1, or a sneaky -0.5), our U-shape flips. It opens downwards. Think of a sad face. 😞 It has a highest point, a maximum. It then just plummets downwards, towards negative infinity, like a dramatic movie scene. 🎬
What if a is zero? Well, then it’s not a quadratic function anymore, is it? It’s just a boring old linear function, a straight line. And straight lines? They go on forever in both directions. Their range is all real numbers, no fuss, no muss. But we’re here for the curves, right?
Finding That Crucial Turning Point: The Vertex
Okay, so that a value is super important for the direction. But to find the range, we need to know the exact lowest or highest point. This magical spot is called the vertex. It’s the tippy-top or the bottom-most part of our U-shape. It’s the turning point, the pivot, the dramatic pause before the graph takes off in the other direction.
There’s a handy-dandy formula to find the x-coordinate of the vertex. Don’t worry, it’s not some ancient riddle. It’s just: x = -b / 2a. Remember those a and b from our ax² + bx + c friends? Yeah, they’re back! Plug them in, do a little division, and voilà! You’ve got the x-value of your vertex.
But wait, we need the y-value for the range, don’t we? Don’t panic! Once you have that x-coordinate, just plug it back into your original quadratic equation. Whatever you get for y? That’s the y-coordinate of your vertex. Easy peasy, lemon squeezy! 🍋
So, let’s say your vertex is at (2, 5). This little coordinate tells you everything about the range. Seriously. It’s like the key to the whole operation.
Putting It All Together: Unlocking the Range
Now for the grand finale! We know the direction (thanks, a!) and we know the turning point (thanks, vertex!). Let’s combine them to nail down the range.
Case 1: The Happy Upward U (a > 0)
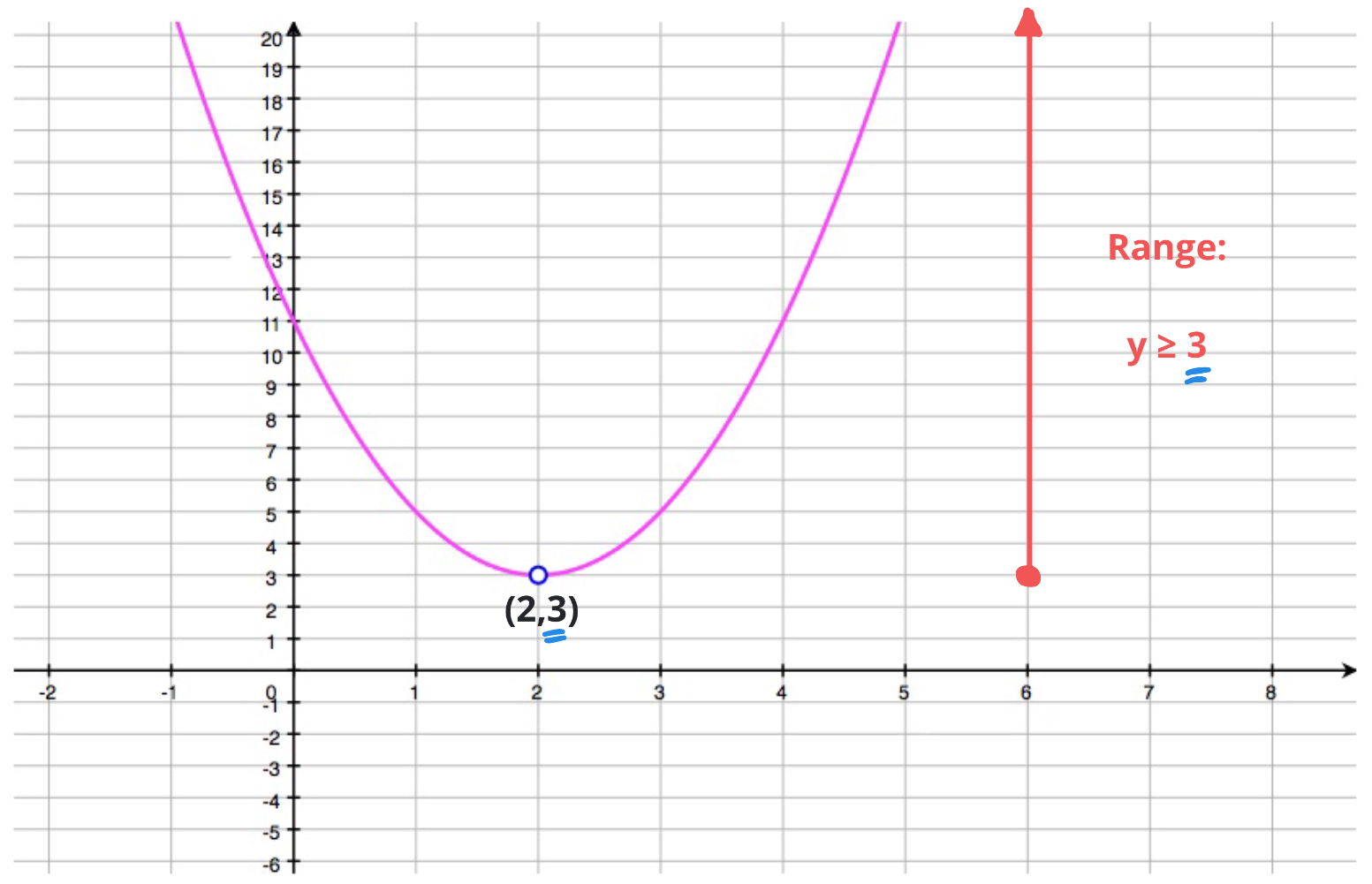
Remember our smiley face? When a is positive, the graph opens upwards. That means it has a minimum point, which is our vertex. So, the lowest y-value the graph can ever reach is the y-coordinate of the vertex. Let’s call it y_v.
Can the graph go any lower than y_v? Nope! It’s the absolute bottom. But can it go higher? Oh, you bet! It shoots up towards infinity. So, all the y-values from y_v and above are part of our range. It’s like saying, "Everything from this point up is fair game!"
In math talk, we write this as: [y_v, ∞). The square bracket means y_v is included, and the parenthesis with the infinity symbol means it goes on forever upwards.
Let’s say your vertex’s y-coordinate is -3. Then your range would be [-3, ∞). All values greater than or equal to -3. See? Not so terrifying.
Case 2: The Sad Downward U (a < 0)
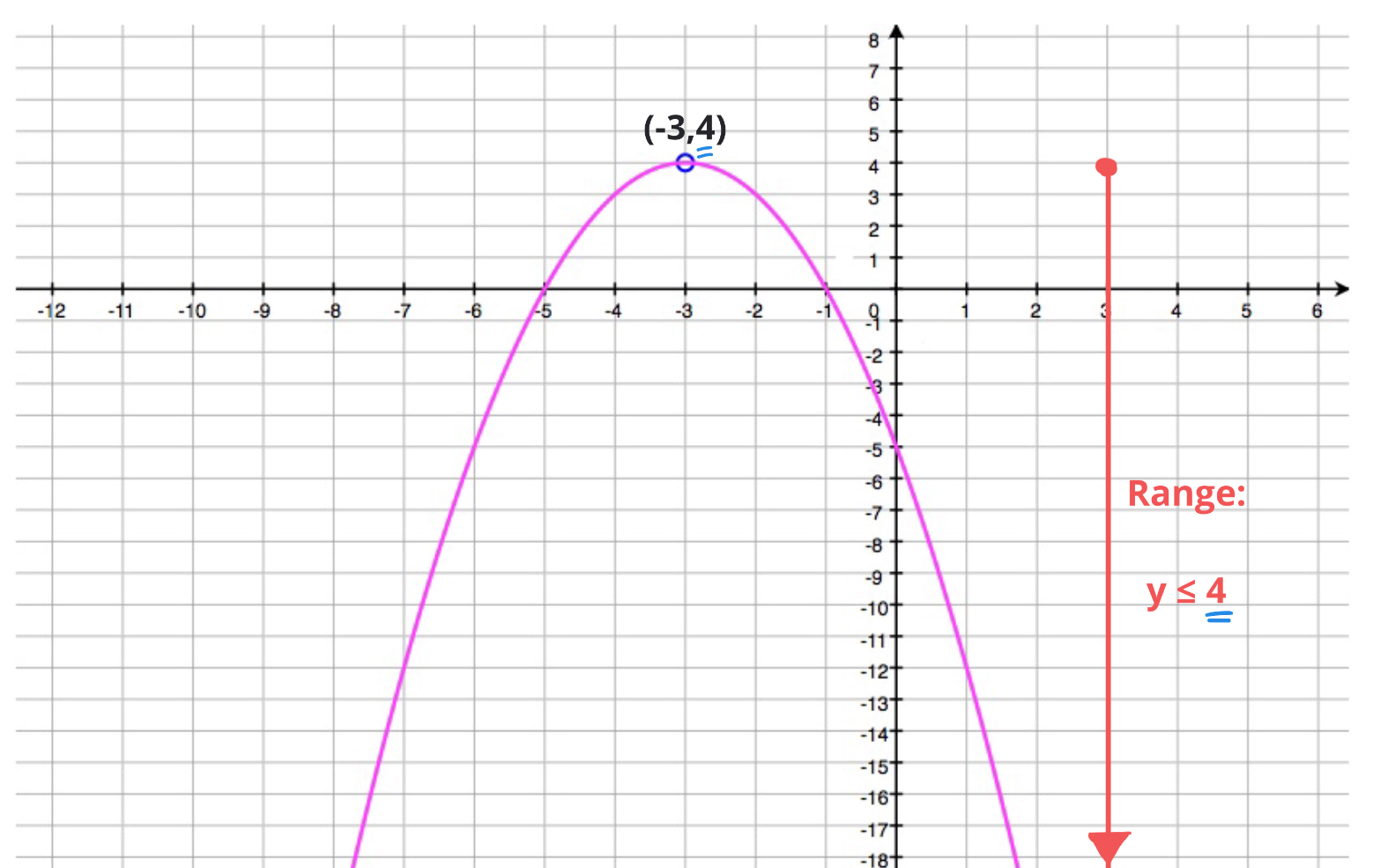
Now, let’s flip it. If a is negative, we’ve got our sad face, opening downwards. This means our vertex is a maximum point. The highest y-value the graph can reach is that y-coordinate of the vertex, y_v. No y-values will ever be higher than this!
But can it go lower? Absolutely! It dives down towards negative infinity. So, all the y-values from negative infinity up to and including y_v are in our range. It’s like, "You can be anything as long as it's not higher than this ceiling!"
In math notation, this looks like: (-∞, y_v]. The parenthesis with negative infinity means it comes from all the way down there, and the square bracket means y_v is included as the highest possible value.
So, if your vertex y-coordinate is 10, your range is (-∞, 10]. All values less than or equal to 10. You're getting the hang of this, aren't you?
Let's Practice! (Because Practice Makes Perfect, Right?)
Okay, time to put on our detective hats. 🕵️♀️ Let's take an example. Suppose we have the function f(x) = x² - 4x + 3.
First things first, what’s our a? It's 1. Since 1 is positive, we know our U-shape is opening upwards. So, we’re looking for a minimum, and our range will be of the form [y_v, ∞).

Next, let's find the vertex’s x-coordinate using our magic formula: x = -b / 2a. Here, a = 1 and b = -4. So, x = -(-4) / (2 * 1) = 4 / 2 = 2. Our vertex is at x = 2.
Now, let’s find the y-coordinate of the vertex. We plug x = 2 back into our original function: f(2) = (2)² - 4(2) + 3 = 4 - 8 + 3 = -1. So, our vertex is at (2, -1).
Since a was positive, the vertex is our minimum. The lowest y-value is -1. And the graph goes up forever from there. Therefore, the range is [-1, ∞). Ta-da! You did it!
Let’s try another one. How about g(x) = -2x² + 8x - 5?
Our a is -2. Uh oh, it’s negative! This means our U-shape is opening downwards. We’re looking for a maximum, and our range will be of the form (-∞, y_v].
Find the vertex x: x = -b / 2a. Here, a = -2 and b = 8. So, x = -(8) / (2 * -2) = -8 / -4 = 2. The vertex is at x = 2.
Now, find the vertex y: g(2) = -2(2)² + 8(2) - 5 = -2(4) + 16 - 5 = -8 + 16 - 5 = 3. Our vertex is at (2, 3).

Since a was negative, the vertex is our maximum. The highest y-value is 3. And the graph goes down forever from there. So, the range is (-∞, 3]. See? You’re a quadratic range wizard now!
What About Those Tricky Forms?
Sometimes, quadratic functions are presented in different forms. Like the vertex form: f(x) = a(x - h)² + k. This one’s actually your best friend for finding the range!
In this form, (h, k) is already your vertex! You don’t even need to calculate it. How amazing is that? If a is positive, your range is [k, ∞). If a is negative, your range is (-∞, k]. Boom! You’re basically cheating the system, but in a good, mathematical way!
What if it's in factored form? Like f(x) = a(x - r1)(x - r2)? This one’s a little less direct for the vertex, but you can still find it. The x-intercepts are at r1 and r2. The vertex’s x-coordinate will be exactly in the middle of these two roots: x = (r1 + r2) / 2. Once you have that x, you plug it back in to find the y-coordinate of the vertex, and then you’re back to our original logic!
The Bottom Line (or The Top Line, Depending!)
So, to recap, finding the range of a quadratic function is all about two things: the direction of the U-shape (determined by a) and the y-coordinate of the vertex. Once you’ve got those two pieces of information, the rest is a piece of cake. Or, you know, a piece of pie. 🥧
Remember, if a is positive, the graph opens up, and the range starts at the vertex’s y-value and goes up to infinity. If a is negative, the graph opens down, and the range goes from negative infinity up to the vertex’s y-value.
Don't let those equations intimidate you. Break them down, find your vertex, check your a, and you'll be a range-finding pro in no time. It’s like learning a secret handshake, but for math! And trust me, once you get it, it feels pretty darn good. So go forth and conquer those quadratics, my friend!