How To Find The Unknown Side Length Of A Triangle

Hey there, puzzle solvers and curious minds! Ever looked at a triangle and thought, "Hmmm, I wonder what that missing side is worth?" Well, get ready for some seriously fun detective work. We're about to dive into the cool world of finding those sneaky, unknown side lengths. It's like a treasure hunt, but with shapes!
Imagine you have a triangle, but one of its sides is a total mystery. It's like a missing piece in a jigsaw puzzle. You've got clues, though! Maybe you know the lengths of the other two sides, or perhaps you know some angles. These are your breadcrumbs leading you to the answer.
There are a few special tools in our triangle toolbox. Think of them as magic wands that help us uncover the secret side. The first one we'll peek at is a real classic. It's perfect for triangles that have a nice, square corner. You know, the kind that looks like the corner of a book or a room.
The Super Star: The Pythagorean Theorem!
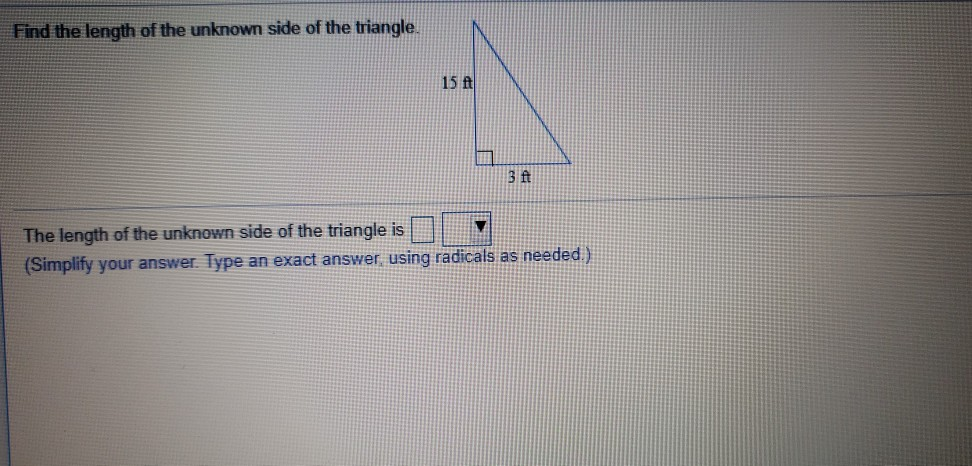
This is where things get really exciting. For those special triangles with a 90-degree angle, we have a super-duper rule called the Pythagorean Theorem. It's named after a very clever ancient Greek dude named Pythagoras. He figured out this awesome relationship.
Basically, if you take the lengths of the two shorter sides of this "right-angled" triangle, square them, and add them together, you get the square of the longest side. It’s like a secret code for right triangles!
Let's say the two shorter sides are "a" and "b", and the longest side (the one opposite the square corner) is "c". The theorem says: a² + b² = c². See? So cool!
Now, what if you know two sides and want to find the third? If you know 'a' and 'b', you can find 'c'. You just do the math: square 'a', square 'b', add them up, and then find the number that, when multiplied by itself, equals that sum. That's your 'c'!

What if you know one of the shorter sides and the longest side? No sweat! You can rearrange the formula. If you know 'a' and 'c', you can find 'b' like this: b² = c² - a². It’s like a puzzle where you have to figure out which piece is missing by looking at the ones you have.
This theorem is so useful, it’s like a superhero cape for math problems. You can find the missing side of any right-angled triangle with just a little bit of squaring and square-rooting. And that, my friends, is super satisfying!
When the Corner Isn't Square: More Awesome Tools!
But wait, what if the triangle doesn't have that perfect 90-degree corner? Don't worry, we're not stuck! There are other fantastic tools for those "non-right-angled" triangles. These are the ones where all the angles are a bit more… relaxed.
One of the stars here is the Law of Sines. It sounds a bit fancy, but it's really just about the relationship between the sides of a triangle and the angles opposite them. It's like a secret handshake between sides and angles.
The Law of Sines says that the ratio of the length of a side to the sine of its opposite angle is the same for all three sides of a triangle. So, a/sin(A) = b/sin(B) = c/sin(C). What does that mean for us?
It means if you know one side and two angles, you can find another side. Or if you know two sides and an angle opposite one of them, you can find another angle. And from there, you can often find the missing side!
You need a calculator that can do 'sine' functions for this one. Don't be scared of the word 'sine'; it's just a fancy way of describing a relationship in a triangle. Your calculator has your back!
This law is great for situations where you have enough information about two sides and angles to set up a solvable proportion. It's like a balanced scale, and you're finding the missing weight.
The Other Big Gun: The Law of Cosines!
And then, we have another powerful tool for our triangle-solving adventures: the Law of Cosines. This one is particularly handy when you know all three sides and want to find an angle, or when you know two sides and the angle between them, and you want to find the third side.

This law is a bit more involved than the Pythagorean Theorem, but it's super versatile. For a triangle with sides 'a', 'b', and 'c', and angle 'C' opposite side 'c', the Law of Cosines states: c² = a² + b² - 2ab cos(C).
See how it's got a little bit of the Pythagorean Theorem in there (a² + b²)? But then it has that extra bit with the cos(C). That's what makes it work for non-right triangles!
If you know the lengths of sides 'a' and 'b', and you know the angle 'C' that's stuck between them, you can use this law to find the length of side 'c'. You just plug in your numbers, do the multiplication, subtraction, and then take a square root.
This law is your go-to when you're given two sides and the angle squeezed right in between them. It’s like building a fence where you know the lengths of two fence posts and the angle they make. You can then figure out how long the connecting fence piece needs to be!

Why Is This So Fun?
So, why is figuring out these missing side lengths so entertaining? For starters, it's like being a detective. You're given a mystery (the triangle with a missing side) and a set of clues (the known sides and angles). Your mission is to use the right tools – the Pythagorean Theorem, the Law of Sines, or the Law of Cosines – to crack the case.
It's also incredibly satisfying. When you finally solve for that unknown side, there’s a little "aha!" moment. It's the feeling of accomplishment when you piece together the puzzle and the triangle makes sense. It’s a small victory that feels great!
Plus, these skills aren't just for math class. Think about building things! Carpenters use these ideas all the time to make sure walls are straight and roofs are the right angle. Architects use them to design amazing buildings. Even when you’re navigating, understanding distances and angles is key!
So next time you see a triangle, don't just see a shape. See a challenge, a puzzle, a chance to use some cool math magic. Grab a piece of paper, a pencil, and maybe a calculator, and try to find that unknown side. You might just surprise yourself with how much fun you have!
Remember, the triangle is waiting for you to reveal its secrets. Go forth and solve!